Motors: KT & KV

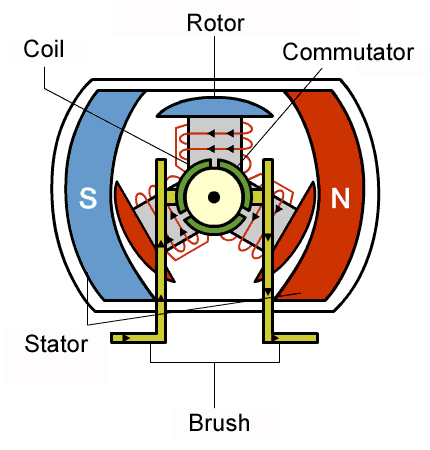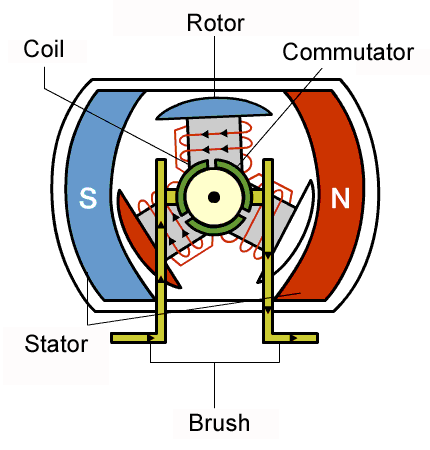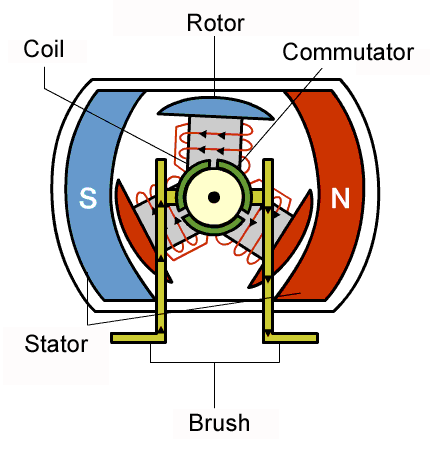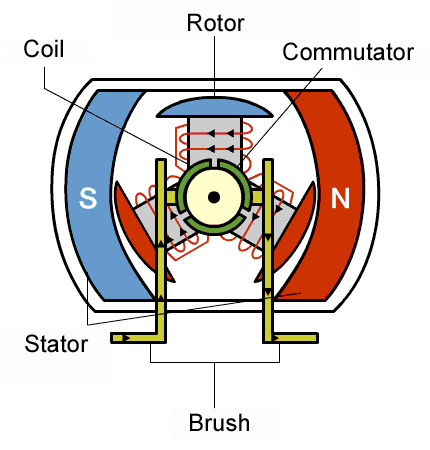
If you pick up the data sheet for a motor, one of the first things you'll see are the $K_V$ and $K_T$ ratings.

A lot of motors even have these values written on the rotor.

But what do they mean?

1. The Relationship Between Torque & Current

Electric motors convert electrical energy into mechanical energy, with torque being the force that causes rotation.

In a simplified DC motor model, the generated torque $T$ is directly proportional to the armature current $I$:

$$T = K_T \cdot I$$

where:

• $T$ is the torque (in Newton-meters, N·m),
• $I$ is the current (in Amperes, A),
• $K_T$ is the torque constant (in N·m/A).

This equation indicates that for every ampere of current, the motor produces a proportional amount of torque as determined by $K_T$.

---

2. The Relationship Between Speed & Voltage

The motor’s speed—typically measured as the angular velocity $\omega$ (in radians per second) or in revolutions per minute (rpm)—is primarily governed by the voltage applied to the motor. As the motor spins, it generates a back electromotive force (back EMF) that is proportional to its speed:

$$V = K_E \cdot \omega$$

where:

• $V$ is the applied voltage (in Volts, V),
• $\omega$ is the angular velocity (in rad/s),
• $K_E$ is the back EMF constant (in V/(rad/s)).

Under no-load conditions, the back EMF nearly equals the applied voltage, linking voltage directly to speed.

---

3. Introducing $K_V$ and $K_T$

$K_V$: The Motor Velocity Constant

• Definition: $K_V$ is typically expressed as the number of revolutions per minute (rpm) the motor achieves per volt under no load.
• Units: rpm/V.
• Interpretation: For instance, if a motor has a $K_V$ of 1000 rpm/V, applying 1 volt ideally produces 1000 rpm, and 10 volts yield 10,000 rpm.

$K_T$: The Motor Torque Constant

• Definition: $K_T$ represents the torque produced per ampere of current.
• Units: N·m/A.
• Interpretation: A motor with a $K_T$ of 0.05 N·m/A will generate 0.05 N·m of torque for every 1 ampere of current.

In ideal motors using SI units, the back EMF constant $K_E$ and the torque constant $K_T$ are numerically equal, reflecting energy conservation within the motor.

---

4. Deriving the Relationship Between $K_T$ and $K_V$

4.1 Converting $K_V$ to SI-Compatible Units

$K_V$ is typically given in rpm/V, but for consistency with SI units (where angular velocity is in rad/s), we need to convert:

$$\omega = \text{rpm} \times \frac{2\pi}{60}$$

If the motor’s speed per volt is $K_V$ rpm/V, then in SI units the speed per volt becomes:

$$K_V^{\prime} = K_V \times \frac{2\pi}{60}$$

4.2 Relating Back EMF to Motor Speed

The back EMF $E$ generated in the motor is given by:

$$E = K_E \cdot \omega$$

Under no-load conditions, the applied voltage $V$ almost equals the back EMF:

$$V \approx K_E \cdot \omega$$

Thus, for a given voltage, the speed is approximately:

$$\omega \approx \frac{V}{K_E}$$

Considering the SI conversion, where the no-load speed per volt is $K_V^{\prime}$:

$$\frac{V}{K_E} = K_V^{\prime} \cdot V$$

By canceling $V$ (assuming $V \neq 0$), we obtain:

$$K_E = \frac{1}{K_V^{\prime}}$$

Replacing $K_V^{\prime}$ with the converted form gives:

$$K_E = \frac{1}{K_V \times \frac{2\pi}{60}} = \frac{60}{2\pi K_V}$$

4.3 Establishing the Relationship with $K_T$

For an ideal motor, energy conservation dictates that the electrical power equals the mechanical power (ignoring losses):

$$I \cdot V = T \cdot \omega$$

Substitute the expressions $T = K_T \cdot I$ and $V = K_E \cdot \omega$:

$$I \cdot (K_E \cdot \omega) = (K_T \cdot I) \cdot \omega$$

Canceling $I$ and $\omega$ (assuming they are non-zero):

$$K_E = K_T$$

Given the earlier result for $K_E$, it follows that:

$$K_T = \frac{60}{2\pi K_V}$$

---

5. Okay... So what?

The main equation care about is this one,

$$K_T = \frac{60}{2\pi K_V}$$

All this equation is saying is that there's a tradeoff between $K_T$ and $K_V$.

And since $K_T$ is proportional to torque and $K_V$ is proportional to speed, then there is a fundamental tradeoff between torque and speed. We can't just increase or decrease both.